Patterns

Mathematicians have known since ancient times that there were only a limited range of regular tessallations capable of covering a plane surface. (By this we mean a repeated, or periodic, pattern than can go on and on in any direction for as long as you like.) In every case we can imagine picking up the entire pattern and moving it along in some direction and dropping it down over itself exactly. In some cases we can also imagine a pick-up, rotate the whole pattern and drop that also leaves the pattern unchanged. Some patterns also look the same if you carefully position a mirror vertically on the page, in a specific locations.

If you limit yourself to using strictly one regular shape we can prove mathematically that only the regular polygons shown below can be involved.

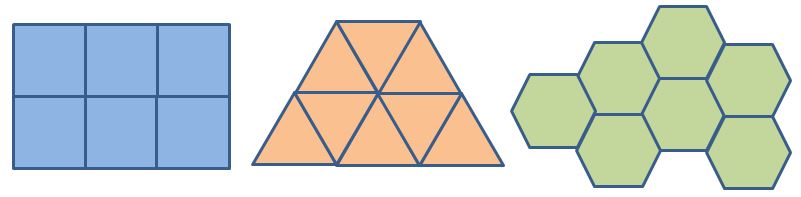
Note how it would be possible to pick up these patterns and translate them sideways, drop them, and get the same pattern. We can also rotate the square tiled pattern by 90^o or 180^o or 270^o (or even 360^o of course) and get back to the same state. The triangles can be rotated through 120^o if you rotate round the centre point of a triangle and 60^o if you rotate round a vertex; the hexagons through 60^o (or 120^o if you rotate round a vertex). You can also look at them in a mirror (or flip them over) in several ways to get back to the same pattern. (That would be true, for example, by putting a vertical mirror on any of the lines in the above diagrams. There are, however, a number of other planes of reflection as well.)

It is therefore specifically impossible to make a regular tiling out of pentagons, and so is not possible to make patterns based on repeating elements that rotate like a pentagon (i.e. through multiples of 72^o).  This is a forbidden symmetry. (But see "Penrose Tiling" below.)

More complicated appearances can be created by allowing ourselves to use two or more shapes (see this article in Wikipedia). We can, of course, also use non-regular polygons, such as rectangles. Islamic art, which avoided representations of the human form, has elaborated the use of regular tiles of different shapes into a sophisticated technique.

All regularly patterns on a 2D surface, however, must be composed of repeats (or translations) in two different directions. This means that there is always a primitive cell which we can reproduce, translate, reproduce, translate in those two directions to fill up the surface. This primitive cell obviously has to be a parallelogram to allow repeated translation in two directions with no gaps. We can, however, choose to think of five types of shapes, with increasing amounts of symmetry. These shapes, illustrated below are known as the basis of five Bravais Lattices.

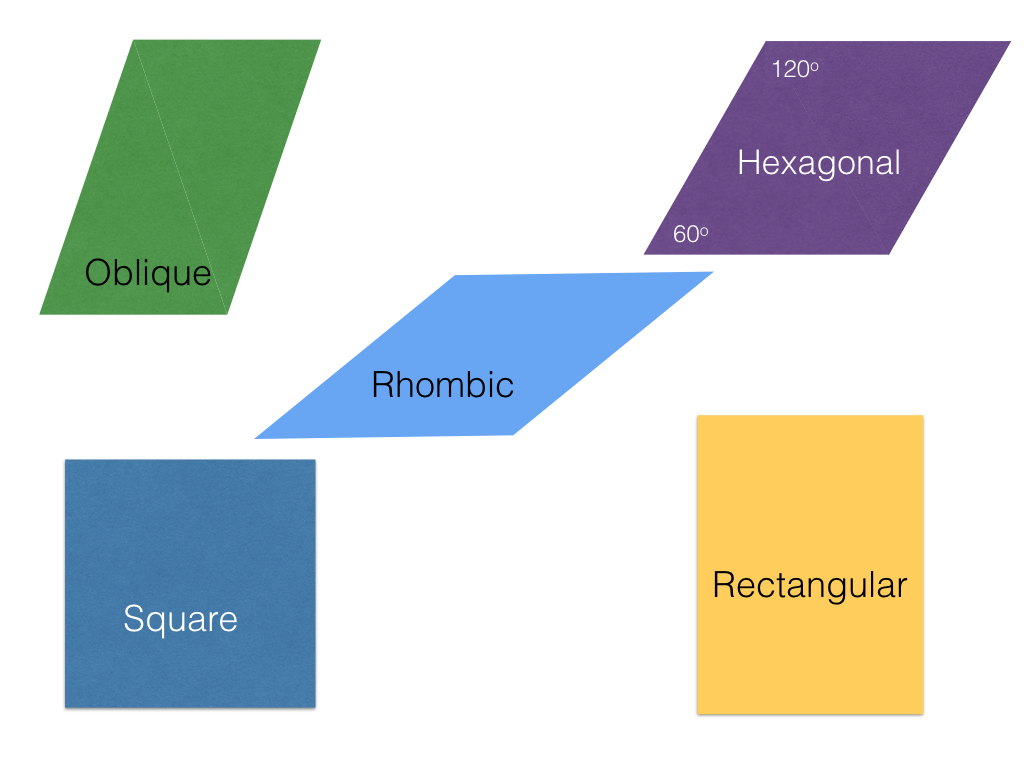
Note that the triangular and hexagonal tilings in the first figure above can be reduced to translations of the quadrilateral unit cell labelled "Hexagonal" in this diagram. (This is obvious in the case of the array of triangles: each pair touching at an edge forms the regular quadrilateral. For the hexagonal tiles, just imagine that each of the hexagons is replaced by six equilateral triangles meeting at a point in the centre.)

Wallpaper Groups

We can also use non-regular polygons, such as rectangles and parallelograms (a rectangle kicked on the head) but mathematics tells use that we will always find that the patterns fall into a small number of categories, just 17, that share the same set of symmetries (in terms of translations, rotations and reflections). These are called the "Wallpaper Groups", because every wallpaper pattern you have ever seen or can ever construct would fall into one of these categories. See this Wikipedia article for a complete catalog of all possibilities.

If you think about filling three dimensional space with regular shapes you get to the "crystallographic groups" that enumerate all the possible ways of making natural crystals. This is a concept of huge importance for the science of materials.

We can build all the possible types of pattern on a two dimensional surface using just four symmetry operations:

• Translation: there will exist two directions in which it is possible to pick up the entire surface, move it by a repeat length along this direction and drop it to find that the pattern is unchanged. This operation (often denoted by the symbol "t") can be repeated as many times as we like in either direction with the same result. We can therefore always draw on our pattern a primitive cell representing the way a pattern can be constructed by repeating the cell. The primitive cell and the two types of translation symmetry have to be present in every wallpaper pattern.
• Rotation: We may also define a subset of wallpaper patterns with rotation centres. We can pick up and rotate the entire pattern around a rotation centre by an angle then drop it to find exactly the same pattern. It can be shown that rotation symmetries can only appear with rotation angles of 60^o,  90^o,  120^o or 180^o (that is, six-fold, four-fold, three-fold or two-fold rotations). If a rotation centre is present in one primitive cell it has to appear in the same place in all the primitive cells.
• Mirror reflections: any pattern is reflected across the mirror plane.
• Glides: - special type of translation. The name is based on the marks made by the action of ice skaters - push forwards (a translation) and the foot goes left, push forward and then the foot goes right. (For those familiar with chess, this is rather like the "knights move".) On the whole, I find that glides are the operations hardest to visualise or recognise.

 It is important to understand that the group to which a pattern belongs is determined by the collection of symmetry operations that are possible on that pattern. Some of the symmetry groups can be expressed as patterns in more than one Bravais lattice - for example, the "p2" group (which has a single two-fold rotation operation in addition to the translations of the lattice) can be expressed on all the Bravais lattices, while "p4" (which has a four-fold rotation) can only be expressed in the square primitive cell. It can be shown, as a fairly straightforward, but not in any way trivial, exercise in Group Theory that there are exactly 17 possible combinations of symmetry operations in the plane. These are illustrated below (as I get round to adding the relevant illustration for each group!).

The conventions for naming groups are not entirely easy to explain and in fact there are several different conventions See this Wikipedia article for an explanation and further references, such as they are. In practice one can just accept the label without explanation.   

The least symmetric type of primitive cell might therefore look something like the example on the right: it is a a regular parallelogram (so it can be repeated indefinitely in either the horizontal direction or a direction a little clockwise of vertical). The unsymmetrical motif, however, means that there are no possible reflection planes or rotational symmetry planes. This is the "P1" group (in an Oblique Bravais cell).  Note that it is possible to create examples of P1 patterns in all the other Bravais cells.
Without the triangle motif we could, of course, find two-fold rotation centres either at any vertex, or the centre of mass of the cell. We can also add this symmetry by reproducing, inverting and carefully positioning the motif,s as in this second example. This is and example of the P2 group (in an oblique Bravais cell). One again, we can create examples of P2 patterns in all the other Bravais Cells.
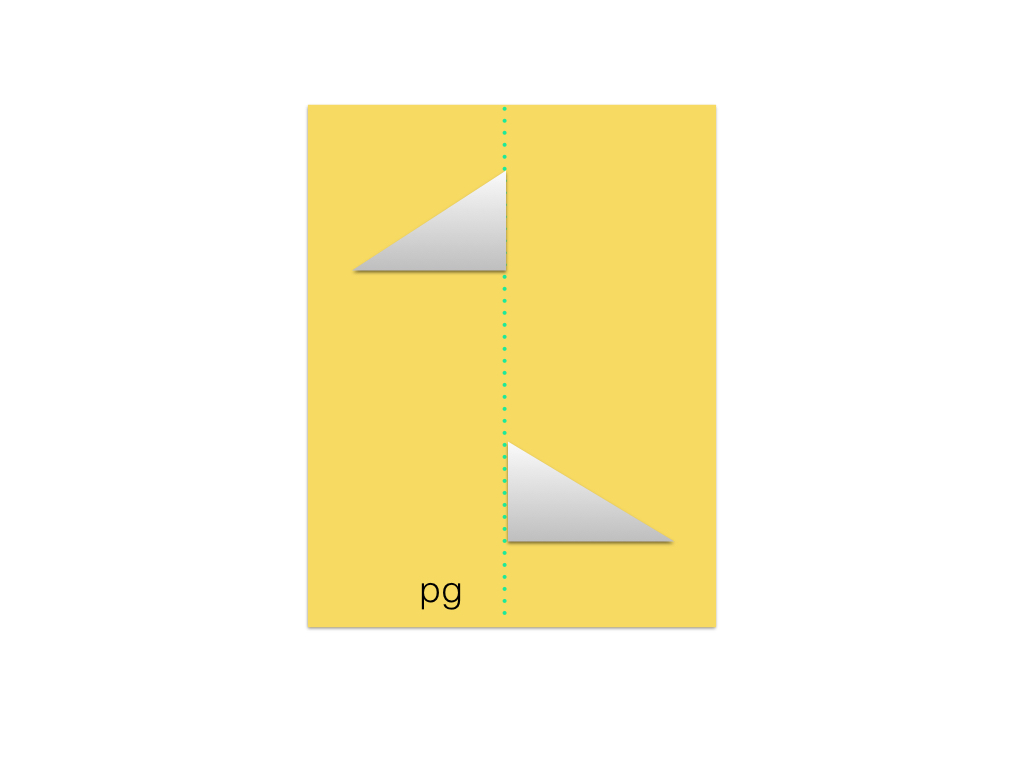
The pg group (in a rectangular primitive cell only). There is, however, an alternative example in which the glide axis is parallel to the short side of the rectangle.
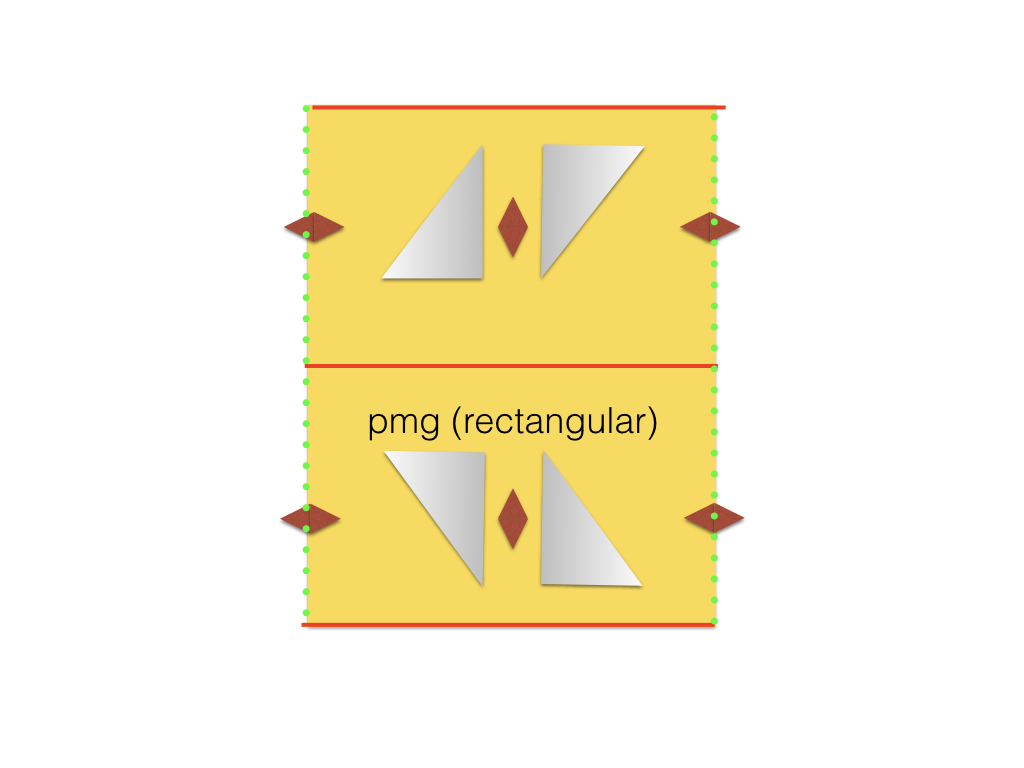
The pmg group always appears in a rectangular primitive cell. There is, however, an alternative example in which the reflection axes are along the long side of the rectangle and the glide planes are parallel to the short side.
The pm group always appears in a rectangular primitive cell. There is, however, an alternative example in which the reflection axes are along the long side of the rectangle and the glide planes are parallel to the short side.
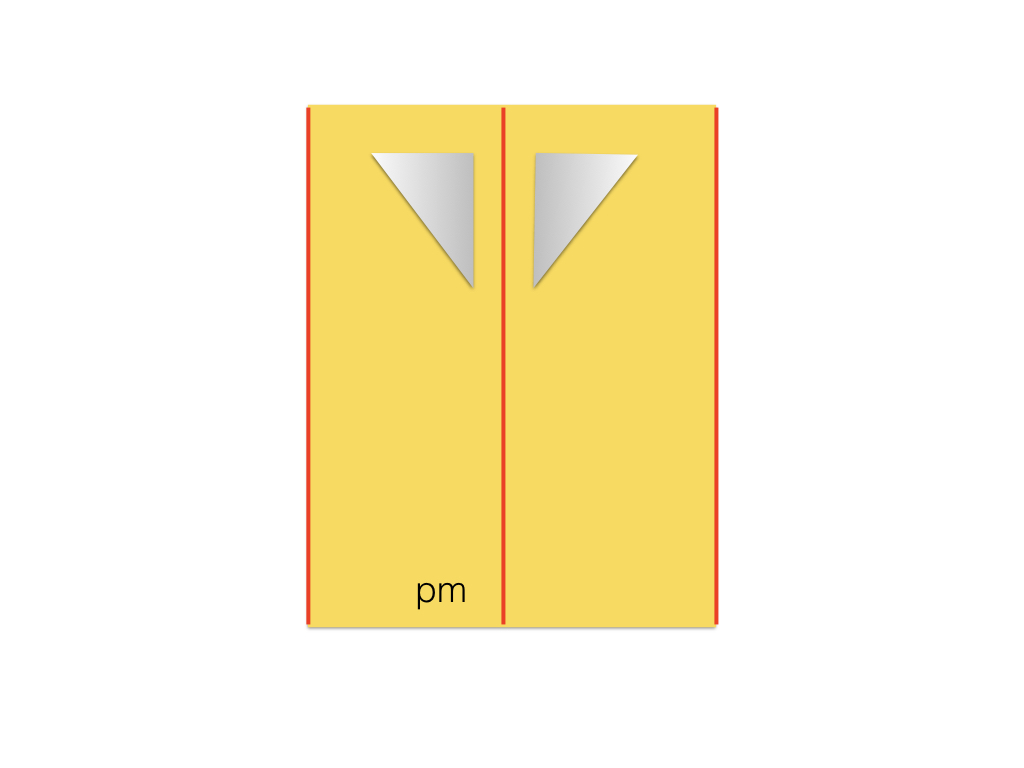The pmm group has two mirror planes at 90 degrees to each other in a rectangular primitive cell. t is also possible to represent this group in the square primitive cell.
The pgg group: always appears in a rectangular primitive cell. There is, however, an alternative example is possible in which the reflection axes are parallel to the short side of the rectangle and the glide planes parallel to the long side. It is also possible to represent this group in the square primitive cell.
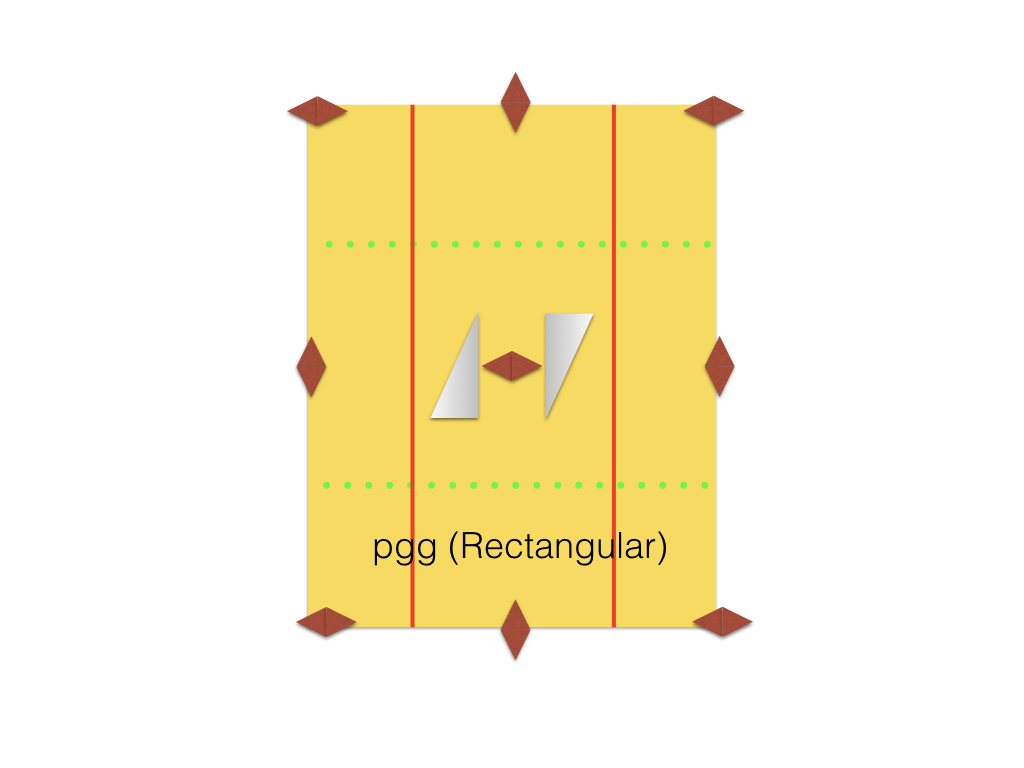The p3 group has three-fold rotation centres, and is only expressible in the hexagonal Bravais cell.
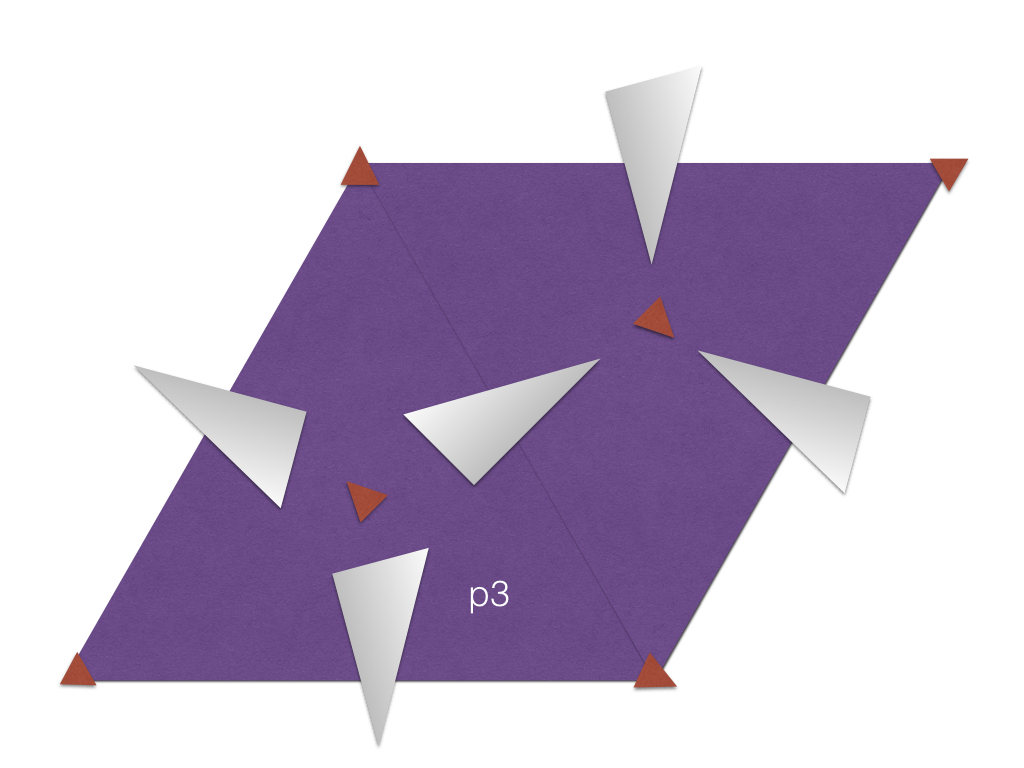The p3m1 group introduces mirror planes through the three-fold rotation centres.
The p31m group has fewer mirror planes.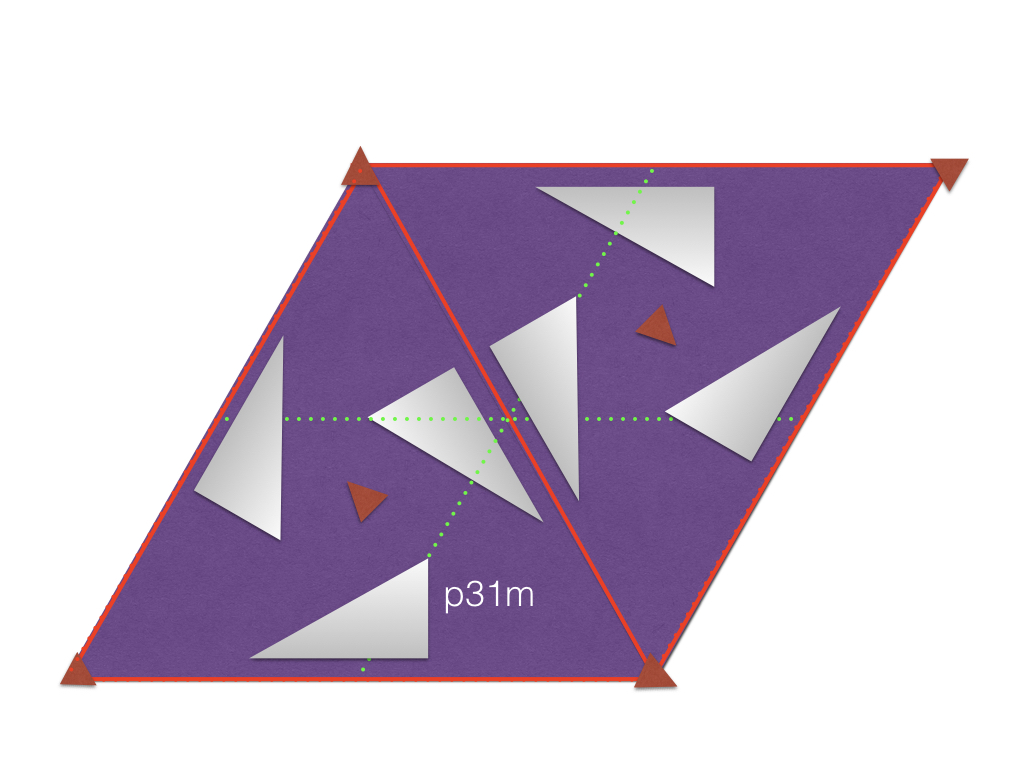
The p4 group has only a four fold rotation axis.
The p4g group also introduces glide planes.
The p4m group has a number of mirror planes.
The cmm group (in a square cell) has two mirror planes at right angles to each other. This group can also be expressed in the hexagonal unit cell.
The cm group is expressed in a hexagonal unit cell. It has one mirror plane and two glide planes. There is, however, an alternative example in which the reflection axes, glide planes and motifs are rotated 90 degrees (i.e. running parallel to the short diagonal).
The example on the right, the p6 group, on the other hand, is a cell with rather a large amount of symmetry, including six-fold rotations. Rotation centres are denoted by the red polygons (hexagonal for six-fold rotation, triangle for three-fold and parallelogram for two-fold). Mirror planes are show by dotted lines. (It is called "hexagonal" because of the six-fold rotation centres - and one could build hexagonal tiles from combinations of this primitive cell.
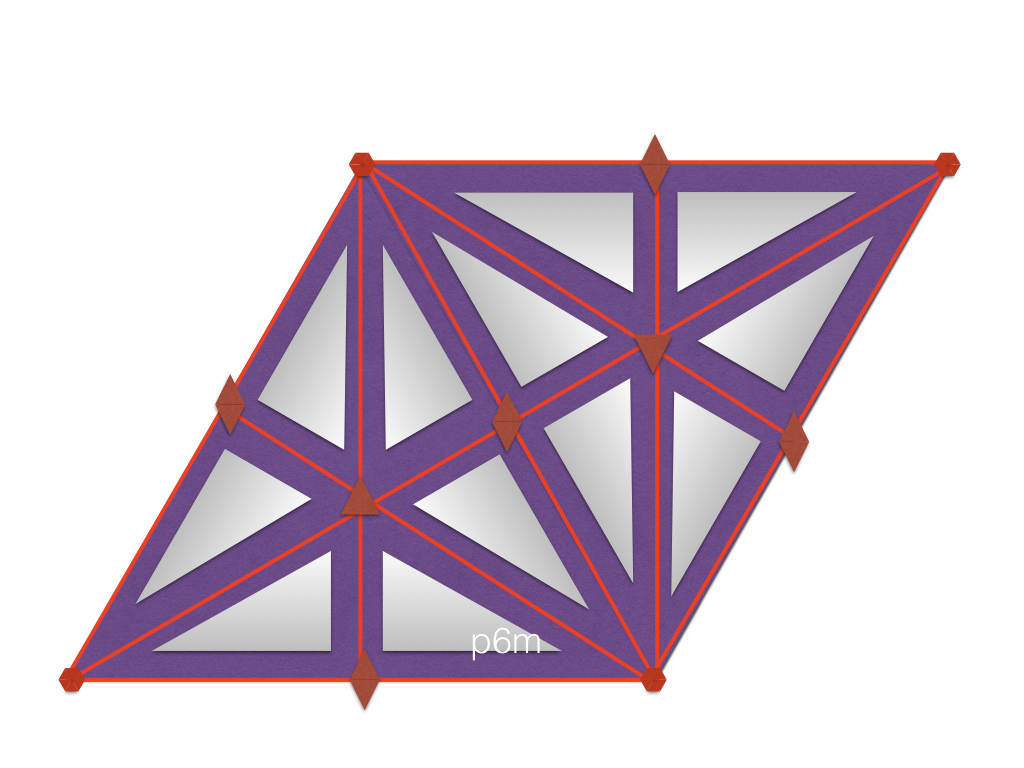
The example on the right, the p6m group, on the other hand, is a cell with rather a large amount of symmetry, including six-fold rotations. Rotation centres are denoted by the red polygons (hexagonal for six-fold rotation, triangle for three-fold and parallelogram for two-fold). Mirror planes are show by dotted lines. (It is called "hexagonal" because of the six-fold rotation centres - and one could build hexagonal tiles from combinations of this primitive cell.  Patterns showing P6 symmetry can only be created on the Hexagonal Bravais cell.

Symmetry arises from placing restrictions on the dimensions and angles of the primitive cell, and also the location of pattern motifs within the cell. This is extremely well explained in the book Creating Symmetry by Frank Farris. (See my Books page.) There are a number of ways of classifying the symmetry of patterns on a 2D surface. (See, for example, the Wallpaper Group page in Wikipedia.) I am labelling my images with the scheme explained by Farris, in which we first look at the number of rotational symmetries and then the mirror planes. So, the first example pattern in the table above is a "p1" pattern, the second a "p2", the third a "p6" - but we can also create "p3" and "p4" patterns, which in practice frequently turn out to be the most visually interesting, and this website contains many examples. 

One could, of course, devise tessellations by directly colouring a single primitive cell to respect the symmetry constraints of a particular group and then reproduce this cell automatically as many times as required to obtain a repeating pattern with the desired symmetry. It is possible to obtain software to do this - and also  "plug-in" modules to systems such as Photoshop and Gimp. Frank Farris provides a different route which in my view often tends to lead more pleasing results. A particular advantage of this approach is that it is easy to break the strict symmetry with straightforward modifications of the functions. I find that this often produces more artistically interesting effects.

I implement some of Dr Farris's methods in my Sketchbooks dealing with Wallpaper Symmetries which are employed to transform original photographic images into patterns displaying the desired amount of symmetry.

The process described by Frank Farris involves constructing a mathematical function (or map) that relates every pixel in the generated image to a pixel in the original image. The mapping is not, however, one-to-one: multiple points in the final image map back to the same pixel in the source image. We deliberately construct the mapping function so that the multiple mapped-to pixels have locations which display the desired amount of symmetry.

Following the logic of this approach requires learning some group theory. The final computational algorithms, however, tend to appear rather less complex since they amount to carefully choosing the coefficients that multiply terms in a summed series of sines and cosines, and you are not aware of the alternative choices that might have been made to give different symmetries. In practice, I have tended to restrict my experiments to rather few of the available wallpaper groups, partly though lack of time. (The code that finally emerges is generally relatively simple, but setting it up to achieve a particular mathematical expression of symmetry is delicate. One has to start from a good understanding of the mathematics.) However, I am also specifically interested in starting with transformed images showing more obvious symmetries (e.g. p3, p3m, p4, p4m and so on) and then deliberately breaking these symmetries in ad-hoc ways (for example varying the transformation parameters as a function of distance from the central point of the image). 

The mathematical theory of symmetries (generally called Group Theory) has many applications beyond designing tiled floors, including solving the Rubik Cube, explaining how chemical molecules interact with electromagnetic waves, and guiding explorations of the fundamental structure of matter. Group theory is one of the main foundations of advanced mathematics, and it all starts from wondering "How may ways to tile a floor?"

Most patterns are patterns because they show various forms of symmetry, and we can invoke symmetry in the generation of new visual constructs (as they do in Islamic art). While many artists develop a good intuitive understanding of symmetry there are also times when it can be useful to have an more explicit understanding. 

Penrose Tiling 

The Wallpaper Groups seemed to be the complete story in two dimensions until Sir Roger Penrose of Oxford University discovered that if you allow yourself to be very slightly non-periodic it is possible to create infinite tessellations that have pentagonal rotational symmetry in any finite region of a tiled plane and any specific arrangement of tiles in one region will be repeated an infinite number of times over an infinite plane. (A lot of intuition-busting maths happens when you allow yourself to think about infinite sets of things.) At some point, however, you will always find a flaw in the regular pattern. These are now known as aperiodic tilings or Penrose tilings, and they have considerably intrigued mathematicians (and some architects) ever since. This knife-edge boundary between regularity and chaos often seems to produce visual structures that are more interesting than either strictly conforming patterns or complete randomness. 

Roger Penrose is an extremely original thinker who explores the boundaries of mathematics and physics (and sometimes psychology and philosophy). He invented mathematical methods used in conjunction with Stephen Hawking to make the seminal discoveries about space time singularities - e.g. black holes - that made both of them well known in the scientific community and beyond, and lead to his share in the 2020 Nobel Prize for Physics.

Sir Roger has always been interested in visual aspects of mathematics - his books tend to be illustrated by his own drawings - and some of the "Impossible Objects" invented in conjunction with his father inspired the graphic art of M C Escher. 

Strangely enough, although Penrose Tilings were invented as a purely intellectual exercise, materials scientists then realised that some natural "quasi-crystals" could solidify into this form - explaining puzzling experimental results, and winning Dan Shectman the 2011 chemistry Nobel Prize. (It just shows that what is not absolutely forbidden tends to happen.)