Mathematicians have known since ancient times that there were only a limited range of regular tessallations capable of covering a plane surface. (By this we mean a repeated, or periodic, pattern than can go on and on in any direction for as long as you like.) In every case we can imagine picking up the entire pattern and moving it along in some direction and dropping it down over itself exactly. In some cases we can also imagine a pick-up, rotate the whole pattern and drop that also leaves the pattern unchanged. Some patterns also look the same if you carefully position a mirror vertically on the page, in a specific locations.
If you limit yourself to using strictly one regular shape we can prove mathematically that only the regular polygons shown below can be involved.
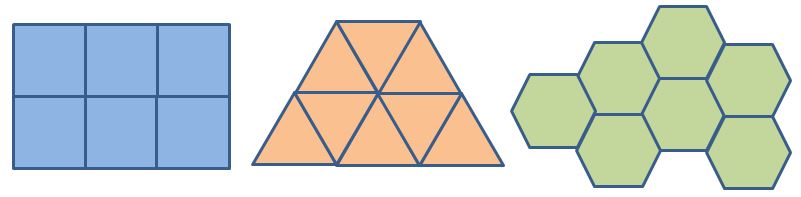
Note how it would be possible to pick up these patterns and translate them sideways, drop them, and get the same pattern. We can also rotate the square tiled pattern by 90o or 180o or 270o (or even 360o of course) and get back to the same state. The triangles can be rotated through 120o if you rotate round the centre point of a triangle and 60o if you rotate round a vertex; the hexagons through 60o (or 120o if you rotate round a vertex). You can also look at them in a mirror (or flip them over) in several ways to get back to the same pattern. (That would be true, for example, by putting a vertical mirror on any of the lines in the above diagrams. There are, however, a number of other planes of reflection as well.)
It is therefore specifically impossible to make a regular tiling out of pentagons, and so is not possible to make patterns based on repeating elements that rotate like a pentagon (i.e. through multiples of 72o). This is a forbidden symmetry. (But see "Penrose Tiling" below.)
More complicated appearances can be created by allowing ourselves to use two or more shapes (see this article in Wikipedia). We can, of course, also use non-regular polygons, such as rectangles. Islamic art, which avoided representations of the human form, has elaborated the use of regular tiles of different shapes into a sophisticated technique.
All regularly patterns on a 2D surface, however, must be composed of repeats (or translations) in two different directions. This means that there is always a primitive cell which we can reproduce, translate, reproduce, translate in those two directions to fill up the surface. This primitive cell obviously has to be a parallelogram to allow repeated translation in two directions with no gaps. We can, however, choose to think of five types of shapes, with increasing amounts of symmetry. These shapes, illustrated below are known as the basis of five Bravais Lattices.
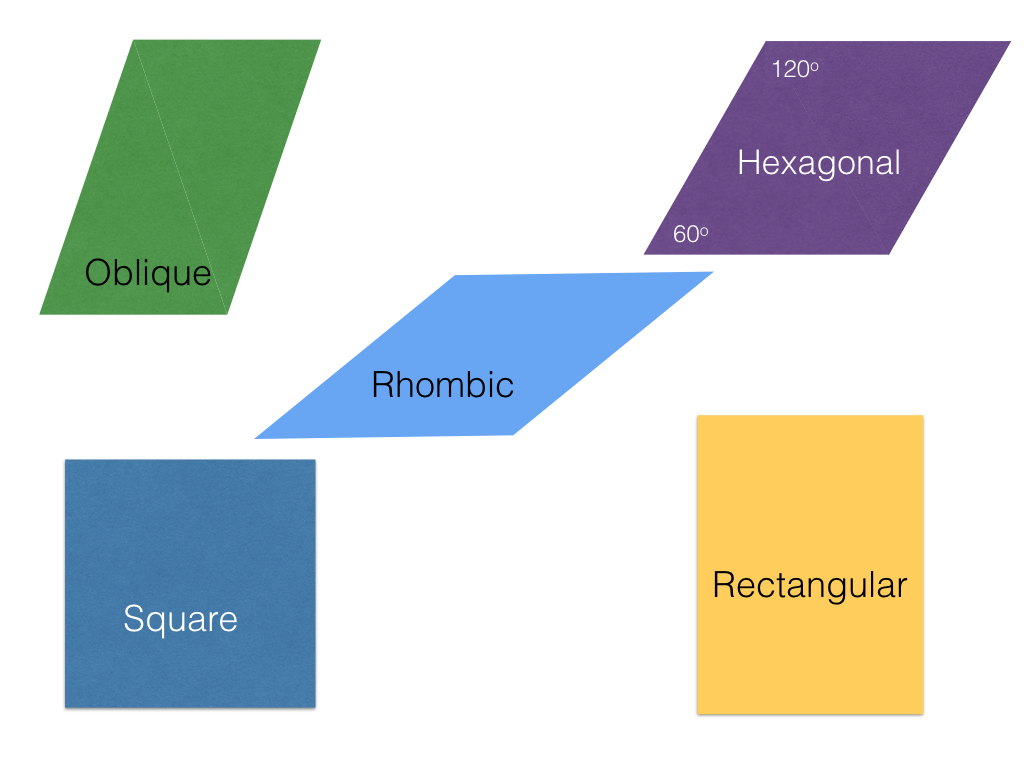
Note that the triangular and hexagonal tilings in the first figure above can be reduced to translations of the quadrilateral unit cell labelled "Hexagonal" in this diagram. (This is obvious in the case of the array of triangles: each pair touching at an edge forms the regular quadrilateral. For the hexagonal tiles, just imagine that each of the hexagons is replaced by six equilateral triangles meeting at a point in the centre.)
