We draw all our figures on a two-dimensional plane, using x and y coordinates. In our epicycles explorations we defined curves in terms of circles rolling round circles and found that in the Processing program we needed to use sums of sines and cosines in sequence of harmonics.
If we now choose to identify the x direction with real numbers and the y direction with imaginary numbers any point in the plane is called a complex number which has a real part and an imaginary part, and using Euler's formular it turns out we can always represent it as R.exp(iθ) and as θ varies from 0 to 2π this formula is just a circle of radius R. So, our epicycles can always be represented mathematically by a formula like:
R1.exp(iθ) + R2.exp(2iθ) +R3.exp(3iθ) + R4.exp(4iθ) ......
which for a mathematician has a very direct connection with the idea of circles rolling round circles. Remember what we just learned in Euler's equation: we can take each of these exponential terms and replace it using:
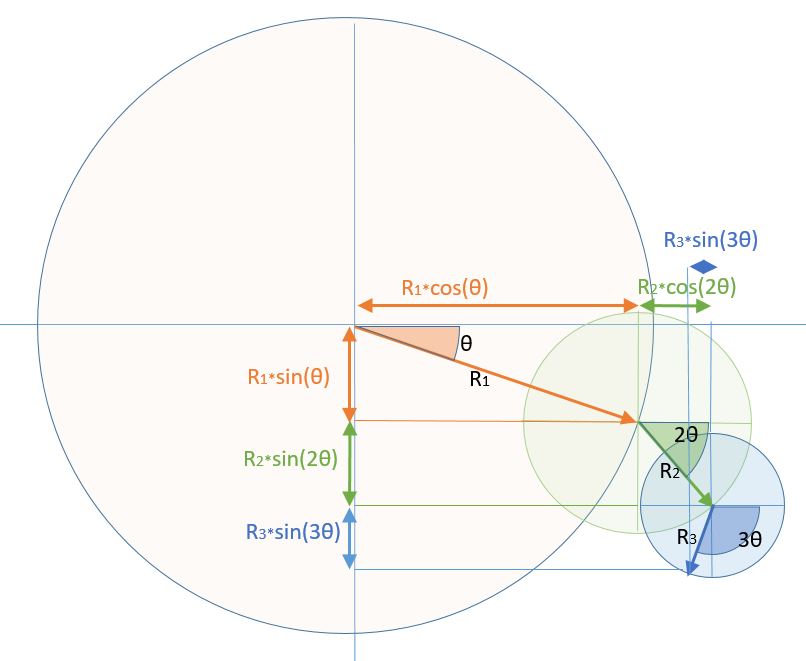
Rnexp(niθ) = Rncos(nθ) + Rni.sin(nθ)
where the "n" represents some selected multiple of the base frequency. Using our elementary trigonometry we can identify Rncos(nθ) with a displacement from the origin in the horizontal plane and Rnisin(nθ) with a displacement in the vertical direction. Adding up all the separate displacements and making small steps in θ gives us a computing recipe for drawing the complex curves. See my Cyclic Motions page for the Processing code.
(You will notice in the diagram below that it is not constructed quite precisely as "circles rolling round circles". I will ask you to take on trust that the diagram below is equivalent and is easier to relate to the equation above. Drawing the "circle rolling round circle" diagram is more complicated and slightly harder to explain. So, since I am not really trying to teach maths, I have left out a somewhat detailed and not very educational step in the argument.)
We can also do things almost immediately with this formula that would be much more confusing when working with the original sines and cosines, such as being able to see quickly what combination of frequencies will give final figures that have particular types of symmetry (such as repeating when turned through fractions of a complete rotation) but for that you will need a bit more maths. (Look it up in the book Creating Symmetry referred to on the Books page.
Surprisingly (again!) one can make just about any closed curve by superimposing epicycles. (This is why the ancient Greeks could represent the motion of the planets with high accuracy in their geocentric astronomy using epicycles, even though the real motions are neither circles nor centred on the Earth.) Look at the figure on the right, which constructs a squarish orbit. (We could make the square as perfect as we wished by adding the more and more smaller cycles - but it would take longer to compute the curve.) See Harmonics and Fourier Series for a bit more discussion of this important technique. For us it means we can produce very complicated curves from simple programs by adding up the right number of frequencies in the right proportions.
So having take a detour through abstract maths and surprising connections, we are back with our original simple geometrical ideas with additional insights.
In our programs, of course, we do not have an easy way to actually represent a partly imaginary number, so we end up back with sines and cosines written separately - but we are now more likely to get all the formulae in the program code correct because we have a better understanding of the patterns.