
Generative Art Techniques
Generative Art Techniques
My earlier explorations of the use of "wave" motifs involved tracing curves based on Lissajous figures. These have an obvious regularity (and are certainly repeating) though it is also possible to make them moderately complex. You may remember that I reached a point where I had started to introduce random elements into the production of the images, and it appeared to me that the results were more visually interesting.
I wanted to move a little further along this path, since it appeared to me that exploring the boundary between order and disorder can create the most visually complex outcomes. But where is the boundary? At what point does randomness go so far that our senses can detect nothing that demands understanding? I need to go a little further.
In that earlier exploration used only one frequency of to-and-fro oscillation in each of the horizontal and vertical axes. As with the explorations of epicycles (or cyclic motions) I could have increased the complexity of the curves by choosing to superimpose a number of different frequencies.
The superimposition of oscillations with different frequencies allows the production of curves with almost arbitrary complexity - providing we recognise that the complete curve always retraces itself at each cycle of the lowest frequency. It seemed to me, however, that it might be worth making the jump to a curve that will never repeat itself, but which nevertheless still carries some degree of order. We can do this by creating a chaotic motion.
The end product of my explorations is shown in the "Generative Waves 13" Gallery - but the story of getting there is complicated.
Evolution of Chaotic Motions
"Chaos" has a very particular technical meaning when used by mathematicians. It is used to refer to dynamical evolutions that are entirely deterministic (that is, completely predictable and reproducible by evolving the equations of motion from the starting condition) but which nevertheless appear to be highly disordered. Let us imaging playing "Poo Sticks". We drop two match-sticks into a turbulent stream very close together at the same time. The sticks, however, will usually quickly start to move on different tracks and after a very short time the motion of one stick will give no clue to the motion of the other stick. Even at the level of water molecules, if we track two that start off as neighbours their motions will soon become completely uncorrelated. This is chaos: motions precisely defined by mathematical equations, but where the smallest possible change in initial conditions become magnified with time (the so-called "Butterfly Effect"). The weather is an excellent example of the practical difficulties of predicting the future of chaotic systems.
Complex dynamics with two gravitational attractors and two test masses that start 1/100 of a pixel apart: click the left mouse button to start at new position, or click the centre button to add a new attractor.
Chaos appears even in apparently very simple systems. One of the first to be discovered was connected with the interactions of a predator and a prey populations that become unpredictable when the interactions are strong. I, however, want a relatively simple two dimensional problem (since I aim to produce a 2D curve). My astronomical history suggested the possibility of tracking the orbit of a small test mass between two larger gravitational attractors. For a range of initial condition (i.e. where we let the test mass go free) the subsequent motion is chaotic, yet confined within a clearly proscribed area of the plane. It appeared to me that this would be a pretty straightforward route to a chaotic motion with all the right characteristics. An example is shown above. (If it does not run in the browser window, which must have Javascript enabled, download the program here and run in Processing to see it evolve).
In fact, it was a little more technically challenging that I had anticipated, and I had to relearn some computing techniques that I once had at my fingertips, but have not practiced for many years. (It turned out that I could have multiplied the complexity of the Lissajous curves to a very high degree much more easily - but there is just something fascinating about non-repeating patterns based on natural phenomena, an additional quality that I cannot entirely explain, but which may be due to the semantics that are associated with the visual evolutions.) The issue centered around well known problems of solving mathematical equations approximately with numerical methods - particularly systems which have a tendency towards chaos anyway.
Predicting the Future is Hard
Consider the problem of navigating a spacecraft to Mars. We have fired the rockets to leave Earth's orbit and now we want to know where we will end up. The rocket will be pulled by the gravity of Earth, the Moon, the Sun and eventually, when we get sufficiently close, by Mars. We cannot write down an equation that describes the complete motion of the spacecraft: the problem is too complicated. What we can do is to note the direction and speed of the rocket at that instant and then ask where it will be, say, one second later, and we also look at the combination of forces on the rocket and work out how much they will change the speed and direction.
This is in essence how most computational future prediction works (such as weather forecasting, where we follow parcels of air rather than rockets). It is called numerical integration. The problem is that there are small errors involved, because the speed and direction of the rocket has, in reality, been slightly changing, due to the forces, during that one second jump forward in time when we assumed nothing was changing. Unless we are rather careful, it is all too easy to allow these errors to multiply at each step until the predictions become worthless. An apparently easy fix is making the time steps smaller - say 1/10 of a second. This is definitely an improvement - for a while - but eventually the errors still grow and grow - it just takes longer for the errors to reach the point of being too large for the predictions to be useful any more.
There are, fortunately, well known numerical analysis techniques that can help us keep the errors within reasonable limits so that we produce physically plausible results. (For example, if I follow the path of an isolated planet around a star "physically plausible" means that it exactly repeats an elliptical orbit indefinitely, and respect laws of nature such as conservation of energy and angular momentum.)
I can then use the average of the forces at the current position and my estimated future position to make a new estimate.
I iterate this estimation until until my revised estimates no longer change. This type of technique does not eliminate errors due to using finite time steps, but it can ensure that they do not grow out of control. (It is not intuitively obvious why this should work and the reason it actually works is too complex to discuss here - but it does!)
You do, however, still need to use small enough time steps to ensure that the errors are of an acceptable magnitude.
The implicit correction I use at each iteration is also designed to ensure that the total energy of the test particle (kinetic plus potential energy) remains constant (this, after all, is a fundamental law of nature!). This produces good results - but not perfect. In particular, the angular momentum (which should also be exactly conserved in a simple orbit - another law of nature!) oscillated up and down a little, which meant that the shape of the orbit changed slightly over time. There are well known methods of doing accurate gravitational orbit calculations with more complicated corrections.
However, because I intended to introduce more gravitational attractors that would deliberately make the subsequent evolution of the test particle path much more chaotic - I want the chaos - there seems to be little point in refining the accuracy of chaos for my particular image construction purposes - no one would notice the difference. (You could not, of course, accurately navigation a spacecraft with my program, but then I do not want to. The professionals at NASA and other space agencies have much more complicated software for that.) My program is doing what it needs to do, with a modest degree of complication, sufficient for the purpose without becoming excessively difficult to understand.
Why bother to go even this far? It so happens that without that first level of numerical trickery (e.g. keeping energy conserved) the curves are just not as smooth as one would really expect and you do not need to be a physicist to notice the problem. It is neither physically plausible nor visually pleasing.
See the "Waves 13" gallery and "Complex Dynamics" gallery for additional images.
Code for simulating chaotic dynamics is available here. N.B. This code does not exactly reproduce any of the images on my gallery (though with the right configuration parameters all of the images could in principle be reproduced): it is a framework for experimentation and the state of this file represent the last experiment before upload. As it happens, for this particular series of experiments I have taken no steps to record the configuration parameters used to produce the images, so none of them is strictly reproducible. (Sometimes I prefer this to be the case.)
- Details
- Category: Generative Art Techniques
Hopefully you have already looks at some of the "beginner" level Processing tutorials, such as:
- Hello Processing
- Getting Started
- Processing Overview
- Coordinate Systems and Shapes
- Color
- Trig Primer or this site's Sines, Cosines and All That.
You need to have worked through at least these tutorials to understand what follows, because I will be using techniques from each of them.
The first step in writing any program is to have a clear idea of what you want to achieve. If you do not have any idea of where you want to end up, you are very unlikely to get there. (OK! So journeys in art are often as much about exploration as following a well-defined route from A to B. The point is still valid: you need some initial ideas about where you might find interesting landscapes.)
This project is inspired by memories of a childhood toy - the "Spirograph" (see the Wikipedia entry) which produced designs such as these:

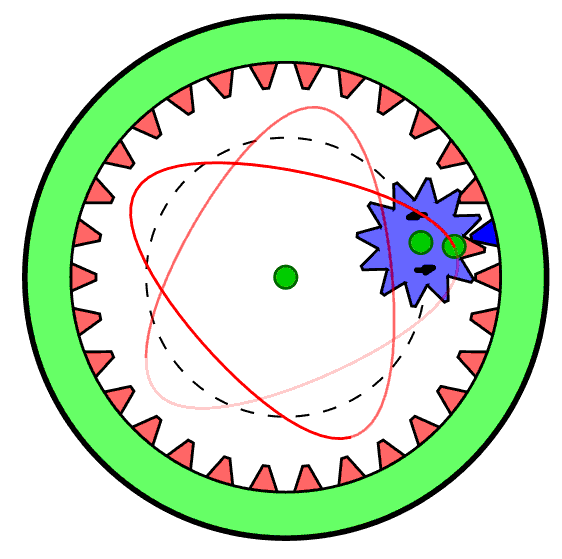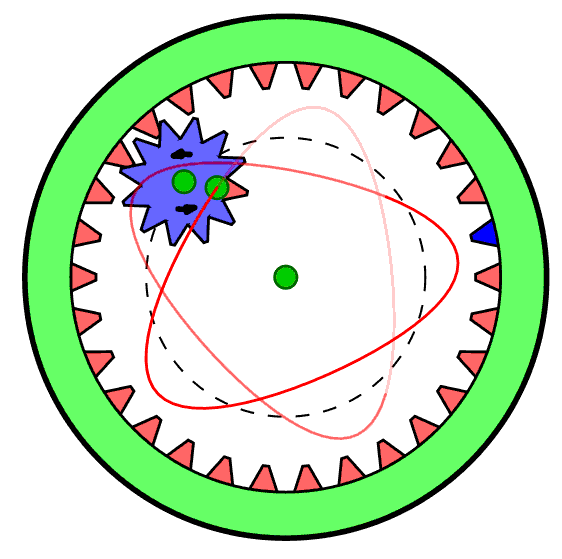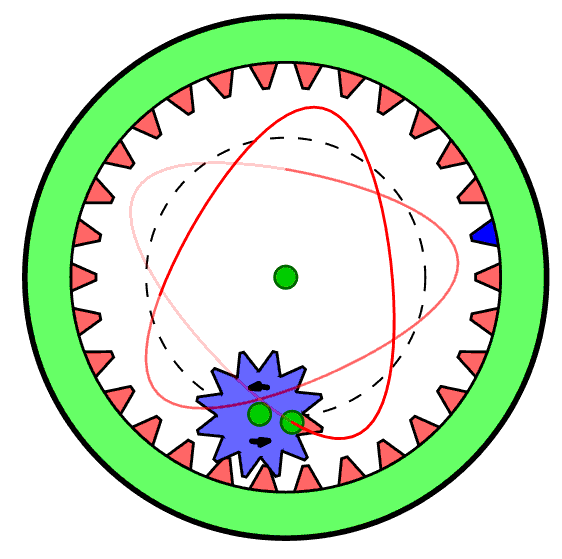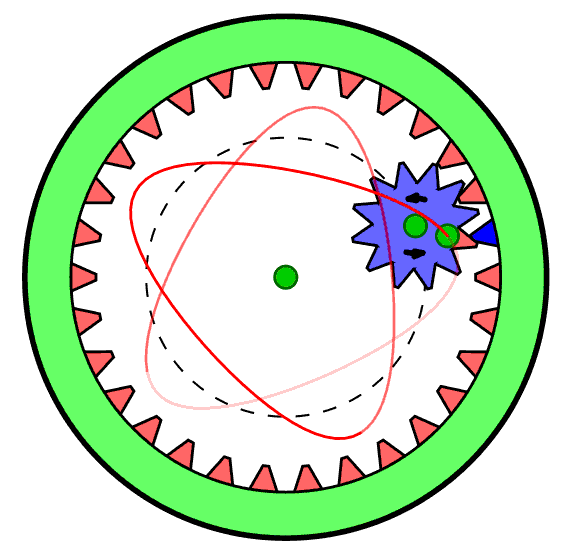
Spirograph was made with plastic gear wheels. By choosing various gear ratios and pen colours one could make a wide variety of figures featuring harmonic motions. (The figure on the right was copied from the Wikipedia page.) Interestingly, Spirograph is still available on the market today, so it still generates visual interest with young people.
Can we reproduce the figures generated by Spirograph using a computer program? (Obviously we can, but how?) This will provide us with a first project to explore how Processing can be used to work our way towards a definite visual goal.
In fact, it will soon become obvious that Processing allows us to go way beyond what was possible with Spirograph. We can, for example, make changing the gear ratios interactive, so we see immediately the effect of different choices. If we wish, we can also make some of the basic parameters vary with time. For example, we can gradually reduce the size of the gears, or we can blend colours rather than switching pens, or we can use nibs with more interesting shapes than a simple point.
Where do we start? We will certainly need to know how to draw a circle. If you have followed the Processing basic level tutorials, you will now know that you can draw a circle using the command such as ellipse(200,200,100,100);. (Reminder: this command says make the (x,y) position (200,200) the center of the figure and make the width and height (200,200), so this produces a circle of radius 100 pixels centred on a point 200 pixels from the left of the window and 200 pixels from the top.)
However, this will not do the trick for us. We need to make small circles run round the inside of big circles, so we are going to need to make them a step at a time as we rotate round the diagram. So, the first thing we need to do is learn how to draw a regular polygon, with a specified number of sides, and we will eventually make the number of side so big that we can no longer see the difference from a proper circle.
float r0 = 150.0; // The radius of our circle in pixels.
int nsides = 12; // The number of side in our regular polygon.
float ith = TWO_PI/nsides; // Increment in angle for each side of the figure.
int x0 = 200; // The centre of the polygon - x coordinate.
int y0 = 200; // The centre of the polygon - y coordinate.
void setup() // Executed once when Processing starts-up.
{
size(400,400); // Size of our canvas.
background(100); // Make the background colour grey.
stroke(255,255,255); // Draw the outline in white.
}
void draw()
{
for(int i=0;i<nsides;i++) // Draw a line for each side
{
float theta = i*ith; // Increment the angle each time round the loop.
int x1 = x0 + int(r0*cos(theta)); // x position of start of each line.
int y1 = x0 + int(r0*sin(theta)); // y position of start of each line.
int x2 = x0 + int(r0*cos(theta+ith)); // x position of end of each line.
int y2 = x0 + int(r0*sin(theta+ith)); // y position of end of each line.
line( x1,y1, x2,y2); // draw the line.
}
}
|
This is the figure (in white) produced by the above program. (The coloured lines and annotations are a later addition, to aid explanation.) Already this simple program introduces a number of important points that need further comment.
|
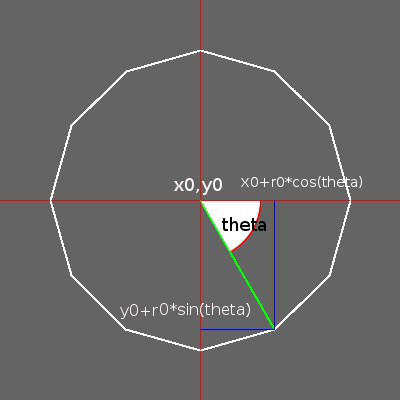 |
So, we now have a method of drawing a polygon that can look as close as we like to a circle. We draw it by allowing the value of theta to go from 0 to 2*π radians. We are going to call this our first harmonic, for reasons that will become clear later.
Things only really start to get interesting when we introduce epicycles that correspond to the smaller gears in Spirograph. We could arrange for another circle to effectively roll around the inside of our first harmonic circle, but this introduces a bit of programming clutter that we do not really need. We can get exactly the same visual effects letting its center move along the circumference of our first-harmonic circle, but rotating from 0 to 2*π twice while we go round the first harmonic once. This is our second harmonic, and we will want to choose its radius to be anything we like. We carry on doing the same thing for third, forth, fifth harmonics and so on, each rotation going 3, 4 or 5 times as fast respectively. We will stop at the ninth for the time being - that is sufficiently complicated already. The program and some of the results are shown in the next page.
The following figure shows how epicycles work.
Instead of using just one sine and cosine to calculate a position on the locus of the epicyclic curve (and getting an approximation to a circle, we add a series of sines and cosines. Each additional term in the sum multiplies our basic iteration angle and the we assign a different radius (a "harmonic amplitude") to each term, getting two summed series which are used to calculate the next X and Y coordinates of the curve:
X = ∑ Rn cos(2π nθ)
Y = ∑ Rn sin(2π nθ)
Now start up Processing and cut and paste the following program into the edit window, and run it to see an animation. (Or else download the complete program here.)
// Variables defined here are "Global" that is, accessible to every sub-program for reading and writing.
// We need to declare here some of the variable whose values will be defined in the setup() routine
// and later used in the draw() routine and its sub-programs.
int xmax; // xmax and ymax will hold the x and y extent of the canvas,
int ymax; // which it is useful to hold in variables so we can refer to them by names.
int xc; // x0 and y0 will define the centre of the canvas
int yc; // which is often useful to refer to by name.
int hmax = 10; // Number of harmonics allows (including zeroth).
float[] r; // The radius of our epicycle harmonics in pixels.
float[] p; // Phases of each harmonic - these will be initialised in setup();
float[] f; // The relative frequency of each epicycle;
int nsides = 500; // The number of side in our regular polygon approximating the circle.
float ith = TWO_PI/nsides; // Increment in angle for each side of the figure.
// Note the use of radians (TWO_PI) for the total angle around a circle.
float tdeg = 180.0/PI; // Conversion factor from radians to degrees.
int count = -1; // For counting the number of times draw() has been called.
float x[];
float y[];
float x1[];
float y1[];
int cr[];
int cb[];
int cg[];
void setup() // Executed once when Processing starts-up.
{
size(1000,1000); // Size of our canvas - has to be explicit integers by Processing rules.
xmax = width; // It is useful to refer to the canvas size symbolically
ymax = height; // so we can remember what we mean when using "400" etc..
xc = xmax/2; // We can now work out the coordinates of the canvas centre.
yc = ymax/2; //
r = new float[hmax]; // Array of harmonic amplitudes
p = new float[hmax]; // Array of harmonic phases
f = new float[hmax]; // The harmonic frequencies.
x = new float[hmax]; // Used to draw the circle radii - x[i] coordinate of current circumference point on i'th circle
y = new float[hmax]; // Used to draw the circle radii - y[i] coordinate of current circumference point on i'th circle
x1 = new float[nsides+1]; // This remembers the x-coordinates of the points used to define the final figure.
y1 = new float[nsides+1]; // This remembers the y-coordinates of the points used to define the final figure.
cr = new int[hmax]; // Array to be used for Red colour component for each harmonic figure.
cg = new int[hmax]; // Array to be used for Green colour component for each harmonic figure.
cb = new int[hmax]; // Array to be used for Blue colour component for each harmonic figure.
for(int h=0;h<hmax;h++)
{
r[h] = 0.0; // Need to ensure that all circle radii are initialised - set all to zero to start with.
p[h] = 0.0; // Phases not used.
f[h] = 1.0+(h-1)*1; // Set frequencies to be n=k*mod(m) to give (m-1)-fold figure symmetry.
cr[h] = 200; //
cg[h] = 200;
cb[h] = 200;
}
r[0] = width/5; // The fundamental size scale;
r[1] = 1.0; // The first harmonic amplitude. (I.e radius of first circle.)
r[2] = 0.8; // The second harmonic amplitude. (I.e. radius of second circle.)
r[3] = 0.4; // The third harmonic amplitude. (I.e. radius of third circle.)
r[4] = 0.2; // The fourth harmonic amplitude. (I.e. radius of fourth circle.)
cr[1] = 0; cg[1] = 0; cb[1] = 200; // Define colour to use for first harmonic circle
cr[2] = 200; cg[2] = 0; cb[2] = 0; // Define colour to use for second harmonic circle
cr[3] = 0; cg[3] = 200; cb[3] = 0; // Define colour to use for third harmonic circle
cr[4] = 0; cg[4] = 200; cb[4] = 200; // Define colour to use for fourth harmonic circle
background(100,100,100);
frameRate(50); // Make this smaller if you want more time to see what is happening.
}
void draw()
{
count++;
translate(xc,yc); // Make origin of coordinate system the centre of the drawing area.
float theta = count*ith; // The angle made from the horizontal by the line
// from the polygon centre to the current vertex.
if(count <= nsides)
{
background(200); // Make the background colour grey - erasing everything
// from the last time draw() was executed.
x1[count] = 0.0;
y1[count] = 0.0;
x[0] = 0.0;
y[0] = 0.0;
for(int h=1;h<hmax-1;h++) // Leave f[9] for perp line
{
stroke(255,255,255,30); // Draw the outline in white.
fill(cr[h],cg[h],cb[h],30); // Fill with a harmonic specific colour specified in setup()
ellipse(x1[count],y1[count],2*r[0]*r[h],2*r[0]*r[h]); // Draw a circle centred at the position specified by the sum of previous harmonics.
x1[count] = x1[count] + r[0]*r[h]*cos(f[h]*(theta+p[h])); // Accumulate the sum of x components of each circle's radius
y1[count] = y1[count] + r[0]*r[h]*sin(f[h]*(theta+p[h])); // Accumulate the sum of y components of each circle's radius
x[h] = x1[count]; // Remember the partial sum so we can draw each circle radius.
y[h] = y1[count];
strokeWeight(3);
stroke(cr[h],cg[h],cb[h],100);
line(x[h-1],y[h-1],x[h],y[h]); // Line from the centre of the current circle to its current circumference point.
}
}
strokeWeight(2);
stroke(255,255,255,100);
for(int i=1;i<=nsides;i++) // Draw (or redraw) all parts of the polygon calculated so far.
{
line( x1[i-1],y1[i-1], x1[i],y1[i]); // draw the line giving one segment of the polygon.
}
}
It becomes a bit tedious to experiment with different figures by varying the amplitude and phase of the harmonics by each time stopping the program, modifying the values defined in setup() and restarting. We can interactively modify amplitudes by adding the following sub-programs. These respond to mouse movement and key-presses and interactively modify amplitudes and phases.
void keyPressed()
{
if(key == '0' ) { r[0] = float(mouseX)/2.0;}
if(key == '1' ) { r[1] = float(mouseX)/float(xmax); p[1] = TWO_PI*float(mouseY)/float(ymax);}
if(key == '2' ) { r[2] = float(mouseX)/float(xmax); p[2] = TWO_PI*float(mouseY)/float(ymax);}
if(key == '3' ) { r[3] = float(mouseX)/float(xmax); p[3] = TWO_PI*float(mouseY)/float(ymax);}
if(key == '4' ) { r[4] = float(mouseX)/float(xmax); p[4] = TWO_PI*float(mouseY)/float(ymax);}
if(key == '5' ) { r[5] = float(mouseX)/float(xmax); p[5] = TWO_PI*float(mouseY)/float(ymax);}
if(key == '6' ) { r[6] = float(mouseX)/float(xmax); p[6] = TWO_PI*float(mouseY)/float(ymax);}
if(key == '7' ) { r[7] = float(mouseX)/float(xmax); p[7] = TWO_PI*float(mouseY)/float(ymax);}
if(key == '8' ) { r[8] = float(mouseX)/float(xmax); p[8] = TWO_PI*float(mouseY)/float(ymax);}
if(key == '9' ) { r[9] = float(mouseX)/float(xmax); p[9] = TWO_PI*float(mouseY)/float(ymax);}
}
The subroutine responds to a key-press, and reads the current position of the mouse. For example, if key "2" is pressed, then the horizontal position of the mouse in the canvas is used to determine a new amplitude of the 2nd harmonic and the vertical position the phase offset. When the "0" key is pressed the horizontal position is used to determine the overall scale of the figure.
We will also find that we want to save images from our programs. In particular, we may want to save an image while a figure is building up over time. To do this we can include the following subroutine.
void keyReleased()
{
// This is called by the Processing system once whenever a key is released.
// The value of the key is stored in the "key" global variable.
// We use the "released" event as a user signal for certain actions
// because we can guarantee that it is a discrete event.
// (In contrast the keyPressed() routine is called multiple times while a key is held down.)
if(key == 's') { saveFrame("Output-####.jpg");} // Save a copy of the current image as a JPEG file.
// The name of the time is constructed according to
// the exact time the event was actioned so multiple
// requests always generate new files.
if(key == 'e') { background(200,200,200);} // Erase the previous figure and create a new background.
}
Pressing the "s" key saves a JPEG image. It will have a name of the form "Output-####jpg" where #### is replaced by a unique integer so we can save multiple images from our program run. The above program also include an erase operation that occurs when the "e" key is presssed.
The following figures show two versions of epicycle generation with interactive control.
| In this sketch, after the curve has finished drawing, you can put the mouse inside the figure click it and then press one of the numerical keys. It will redraw the figure with the amplitude and phase of the harmonic component corresponding the number of the key modified. Moving the mouse left to right changes the amplitude of the harmonic, moving it up and down changes the relative phase. | |
| This figure also draws epicycles, but modifies the complete curve interactively. Again, click with the mouse on the figure, then depress one of the numerical keys and keep it depressed while you move the mouse. It will redraw the figure with the amplitude and phase of the harmonic component corresponding the number of the key modified. Moving the mouse left to right changes the amplitude of the harmonic, moving it up and down changes the relative phase. |
See my Harmonics page for a more in depth discussion of Fourier Series and an further example of using epicycles to produce a square!
Now let us see how we can use this to produce some more interesting images, using a slightly more elaborate program described on the next part.
We now have all the parts in hand. The program below has been used to generate most of the figures in the "Epicycles" Gallery. However, just pressing the "Run" button produces a rather boring image - a fuzzy circle. All we are seeing here is the first harmonic - a circle, where the points that are iterated over on the curve are each given an additional small motif - a short line perpendicular to the curve and one at a tangent to the curve.
Things only become interesting when we start to use the interactive features. That is where you start to add value to the generated image. Outputs from the example program (above) illustrates what is possible. The example program below show how epicycle curves are constructed - this just shows the setup() and draw() parts of the program. (The full program including additional subroutines, keypressed() and keyReleased(), for interactivity and saving images can also be downloaded here.) Just paste it into the Processing code window and run.
// Variables defined here are "Global" that is, accessible to every sub-program for reading and writing.
// We need to declare here some of the variable whose values will be defined in the setup() routine
// and later used in the draw() routine and its sub-programs.
float ampr=50; // Amplitude of variation of RED component of colour.
float ampg=200; // Amplitude of variation of GREEN component of colour.
float ampb=55; // Amplitude of variation of BLUE component of colour.
int r_zero = 10; // Level around which R component varies with amplituded ampr;
int g_zero = 100; // Level around which G component varies with amplituded ampg;
int b_zero = 200; // Level around which B component varies with amplituded ampb;
float p_red = 0.7; // Number of radians that takes R component through its full range of variation.
float p_green = 0.8; // Number of radians that takes G component through its full range of variation.
float p_blue = 0.9; // Number of radians that takes B component through its full range of variation.
float dpr;
float dpg;
float dpb;
int xmax; // xmax and ymax will hold the x and y extent of the canvas,
int ymax; // which it is useful to hold in variables so we can refer to them by names.
int xc; // x0 and y0 will define the centre of the canvas
int yc; // which is often useful to refer to by name.
int hmax = 10; // Number of harmonics allows (including zeroth).
int hmode = 0;
float[] r; // The radius of our epicycle harmonics5 in pixels.
float[] p; // Phases of each harmonic - these will be initialised in setup();
float[] f; // The relative frequency of each epicycle;
int nsides = 10000; // The number of side in our regular polygon approximating the circle.
float ith = TWO_PI/nsides; // Increment in angle for each side of the figure.
// Note the use of radians (TWO_PI) for the total angle around a circle.
float tdeg = 180.0/PI; // Conversion factor from radians to degrees.
int count = 0; // For counting the number of times draw() has been called.
void setup() // Executed once when Processing starts-up.
{
size(1200,1200); // Size of our canvas - has to be explicit integers by Processing rules.
xmax = width; // It is useful to refer to the canvas size symbolically
ymax = height; // so we can remember what we mean when using "400" etc..
xc = xmax/2; // We can now work out the coordinates of the canvas centre.
yc = ymax/2; //
r = new float[hmax]; // Array of harmonic amplitudes
p = new float[hmax]; // Array of harmonic phases
f = new float[hmax]; // The harmonic frequencies.
dpr = TWO_PI/p_red; // Increment of RED phase
dpb = TWO_PI/p_blue; // Increment in BLUE phase
dpg = TWO_PI/p_green; // Increment in GREEN phase
for(int h=0;h<hmax;h++)
{
r[h] = 0.0;
p[h] = 0.0;
f[h] = 1.0+(h-1)*5; // Set frequencies to be n=k*mod(m) to give (m-1)-fold figure symmetry.
}
r[0] = width/5; // The fundamental size scale;
r[1] = 1.0; // The first harmonic amplitude. The rest initialised to zero in setup();
r[9] = 0.1;
background(200,220,220);
stroke(255,255,255,50); // Draw the outline in white.
}
void draw()
{
count++;
translate(xc,yc); // Make origin of coordiante system the centre of the drawing area.
//background(100); // Make the background colour grey - erasing everything
// from the last time draw() was executed.
//r[0] = r[0]*0.995;
for(int i=0;i<nsides;i++) // Iterate round the vertices of the polygon approximating a circle
{
float theta = i*ith; // The angle made from the horizontal by the line
// from the polygon centre to the current vertex.
// Define current rgb colour
int red = r_zero +int( ampr*sin( dpr*theta ) );
int blue = b_zero +int( ampb*cos( dpb*theta ) );
int green = g_zero +int( ampg*sin( dpg*theta ) );
float x1 = 0.0; //
float y1 = 0.0;
float x2 = 0.0;
float y2 = 0.0;
float x3 = 0.0;
float y3 = 0.0;
//if(pflag == -1 && i == 0) {pflag = 1;}
for(int h=1;h<hmax-1;h++) // Leave f[9] for perp line
{
x1 = x1 + r[h]*cos(f[h]*(theta+p[h]));
y1 = y1 + r[h]*sin(f[h]*(theta+p[h]));
x2 = x2 + r[h]*cos(f[h]*(theta+p[h]+ith));
y2 = y2 + r[h]*sin(f[h]*(theta+p[h]+ith));
x3 = x3 + r[h]*cos(f[h]*(theta+p[h]+ith*2));
y3 = y3 + r[h]*sin(f[h]*(theta+p[h]+ith*2));
}
x1 = x1*r[0]; y1 = y1*r[0];
x2 = x2*r[0]; y2 = y2*r[0];
x3 = x3*r[0]; y3 = y3*r[0];
stroke(255,255,255,5);
line( x1,y1, x2,y2); // draw the line giving one segement of the polygon.
// The geometry here is not trivial, it is about finding the angle of bend
// at each vertex of the polygon and then bisecting it to draw a line perpendicular to the curve,
// and also establish tangent lines at right angles to the perpendicular.
// Expect to have use your large-size thinking cap if you want to work out what is going on here.
float theta1 = atan2((y2-y1),(x2-x1)); if(theta1 < 0.0) { theta1 = TWO_PI+theta1;};
float theta2 = atan2((y3-y2),(x3-x2)); if(theta2 < 0.0) { theta2 = TWO_PI+theta2;};
float dtheta=theta2-theta1;
if(theta2 > theta1)
{
dtheta = PI+theta2-theta1;
}
else
{
dtheta = TWO_PI+PI + theta2-theta1;
}
if(dtheta < 0.0) {dtheta = TWO_PI - dtheta;}
float alpha = PI-dtheta/2.0;
float x4 = x2 + r[0]*r[9]*cos( theta1 -alpha ) ;
float y4 = y2 + r[0]*r[9]*sin( theta1 -alpha ) ;
float x5 = x2 + r[0]*r[9]*cos( theta1 -alpha - HALF_PI) ;
float y5 = y2 + r[0]*r[9]*sin( theta1 -alpha - HALF_PI ) ;
float x6 = x2 + r[0]*r[9]*cos( theta1 -alpha + HALF_PI ) ;
float y6 = y2 + r[0]*r[9]*sin( theta1 -alpha + HALF_PI ) ;
stroke(red,green,blue,5);
line( x2,y2, x4,y4); // Make a line perpendicular to the curve.
line( x2,y2, x5,y5); // Make for rearward moving tangent line.
line( x2,y2, x6,y6); // Make a forward moving tangent line.
}
}
The first thing we may wish to do is adjust the amplitudes of the higher harmonics, by pressing the numerical keys and moving the mouse. Note that the images overlap while we are doing this. (We can erase and start again by pressing the "e" key.) The "0" key changes to overall scale of the figure and in this implementation the "9" key changes the size of the motif drawn at each point on the curve.
You can alter the length of a perpendicular line drawn at each point on the curve by holding down the "p" key and moving the mouse, and a tangent line to the curve with the "t" key and mouse. Note that the lines are drawn with a low opacity so the figure takes time to build up.
All the figures in the gallery are produce by interactive manipulations of these keys, and saved by pressing the "s" key. None of the figures are easily reproducible in that one would need to follow the same set of interactive operations exactly. You must experiment to see what can be achieved (and it is a surprising variety of forms).
You might like to play around with the line in setup() that says "f[h] = 1.0+(h-1)*5;". This expression has the effect that when we press the "3" key we are not getting the third harmonic, but one with frequency multiple defined by "1+ (3-1)*5", that is, 11. If we press the "4" key we get a frequency multiple "1+(4-1)*5", or 16. The "5" in this expression guarantees a five-fold symmetry in the final figure. Changing it to 3 or 4 or 6 or 11 would give higher rotational symmetries.
You might also like to play with the configuration parameters that affect the cycling of the colours.
Experiment!
What you need to do now is understand each line of the example above, and then try making some changes to achieve different effects.
The major characteristic of these epicyclic curves is that for each frequency component with have a cosine function controlling motion in the x direction and a corresponding sine function (that is, a cosine with a 90o phase shift) of the same frequency and amplitude controlling motion in the y direction. Things can get interesting if the allow the amplitudes and the phases to be different. We get Lissajous Curves. This is the subject of my next investigation - this time inspired by memories of playing with oscilloscopes and signal generators during lab work.
- Details
- Category: Generative Art Techniques
This is not an original idea: I saw a photographic example in an article on computational photography in a technical journal, and worked out how to do it myself.
There are three steps involved in making bendy-door images:
- Video yourself coming through a door, from the other side, going through the motions of opening walking through and closing it.
- Use a software tool to split the video into separate frames (hundreds of them!).
- Use a Processing program (see below) to take one line from each frame and paste it sequentially into the final image.

- Details
- Category: Generative Art Techniques
We all know that absolutely regular patterns are not very common in the natural world around us. The exceptions are unusual enough attract attention, for example, the regular hexagons of wax forming the brood cells in a beehive. (There is a good mathematical explanation for this particular regularity: it uses the smallest amount of wax to form the maximum number of cells: so bees evolved over time to optimise their use of resources in producing the maximum number of young.) Similarly, natural crystals arise from the underlying regularity of the way atoms pack together at the microscopic level.

Every tree, however, looks a bit different to its neighbour - even if that neighbour is a genetic clone. Yet, the shape of an oak tree is recognisably different to the shape of an ash or a maple. An artist can draw a tree from his imagination and it will look like a tree (and, if he or she is an observant artist, it may look specifically like an oak tree or specifically like an ash tree). There is, in fact, something about such natural forms that remains characteristic even when every natural example is a distinctly different randomly structured individual.
The concepts of fractal geometry help to capture some of these characteristics.
Let us look at the tree again, and measure the total length of all the branches and twigs. From a distance we see only the thickest branches and our measurement will reflect the detail we can see. As we move closer we see thinner branches and the length we measure increases. When we are close, we now see fine twigs and the length we measure increases again.
It is the same with coastlines: from space we measure one value for the length of the UK coastline, from a plane a somewhat longer length because we can see the wiggles on a finer scale, and walking the coastline we see even more convolutions and increase our length estimate again. If we had a microscope we would see even more normally invisible wiggles. It has (we would now say) a "fractal" structure.
Mandelbrot captured this phenomenon by introducing the idea of a "fractional dimension" (he also called it the "art of roughness"). If we double the size of a square the length of the perimeter would increase by a factor of two (and the area by a factor of four). However, if we take the UK coast line and halve the size of our measuring ruler then the estimate of its length would change by a factor somewhere between one and two. That value - the fractional dimension - measures something very characteristic about the visual quality of the convoluted coast line. Mandelbrot called fractal geometry the geometry of nature.

Fractal Clouds over a Fractal Landscape?
It also means that we can use fractal geometry to generate images that have some characteristics of shapes we see in nature. It appears to be the case that many people viewing such images find them more pleasing than either highly regular patterns, or images with a high degree of irregularity. I suspect we respond to the characteristics which resonate with natural structures, even though we may not recognise them explicitly. (It may even be that our brains are wired to recognise fractal characteristics at some level, having evolved as a means of efficient recognition of the irregular patterns of the natural world.)
Most people have probably encountered images based on calculations of the Mandelbrot Set, but this is only one example of a fractal structure. There are many algorithms and variations that can be used in the production of generative art. I aim to explore some the possibilities.
My first exploration is, of course, the Mandelbrot Set itself. Why? Because it is easy to generate highly decorative results: small effort and high reward.
- Details
- Category: Generative Art Techniques
I have already explored image transformations using Complex Maps - that is, we treat the final image plane as a complex (or Argand) plane, and then apply to each pixel location a complex mapping function in order to derive a further complex number which is used to reference a point in the original source image.

The inspiration for this comes from the book Creating Symmetry: the Artful Mathematics of Wallpaper Patterns, by Frank Farris. In the Complex Maps series I used a technique from one of the earlier chapters in this book - "Rosette Functions" - modified somewhat to my own requirements. The work discussed on this page uses the methods discussed in a later chapter to produce patterns with "Wallpaper Group" symmetries.
"Wallpaper Groups" are the seventeen "point groups" that classify all the possible symmetries of patterns on a 2D surface. (See the Patterns on a Surface page. )Here, however, we start by selecting a group with 3-fold rotation symmetry. Frank Farris then shows us how to construct a complex mapping function that have the symmetry of this group.
The fundamental idea is to think of a complex wave function expressed in the conventional form exp(2πiy) which is varying in the y direction.To this we can add equivalent waves with directions rotated by 120º and 240º, so producing a function that exhibits the required symmetry. I
Because this is a wave form, it also has translational symmetry as well as rotational symmetry.
Actually, in my first attempts to implement this algorithm the final images (see figure on the right) turned out not to have an obviously apparent 3-fold rotational symmetry. That was the result of adapting the program used in the previous Complex Maps exercise, in which the source image is addressed by an x,y coordinate system with the range (-1,1) in both directions, regardless of whether the original image is square or rectangular. By default in the earlier program I create an output image with the same relative scale as the original. There is a good reason for this: I wanted to see a smooth transition from the undistorted original (i.e. a 1:1 mapping between equivalent pixel locations) and images in which varying amounts of the higher harmonics have been added. I still wanted to be able to do this, by adding an Aoz to the above formula, permitting Ao to be decreased to 0 as other harmonic amplitudes are increased. Getting true threefold rotation will require some careful scaling of coordinates.
As it happens, I tend to think that the unintended results are visually OK, thought they are in fact examples of a different symmetry group. Sometimes I find that perfect symmetry detracts from the aesthetic appeal. Hence, I break the symmetry in two different ways: firstly, by adding in that zeroth harmonic component - the original image; secondly, by applying a function that varies the harmonic amplitudes across the plane of the image. When using this modification we do not see strict translational symmetry; though the primitive cell is still present and uniformly sized a slightly different transformation generates the pattern in each cell. (Frank Harris demonstrates a similar technique in his book, though I apply a different functional form to vary amplitudes.)
- Go to the p3m Wallpaper Symmetry page for a discussion of how to produce images with 3-fold symmetry.
- The p4m Wallpaper Symmetry page deals with 4-fold symmetry
The Processing programs used to produce these images will be uploaded and linked after a little more tuning - in particular getting the true threefold rotation to work when required. It contains the code for producing evolving image sequences, but you need to provide the algorithm that adjusts the transformation parameters through time.
As always, I expect those who use these programs to make some effort to understand how they work. The video sequence actually includes a number of clips produced separately, using different types of transformation. (For example, a simulation of raindrops on a water surface - see right - which is documented separately.)
- Details
- Category: Generative Art Techniques
